In my last post I pointed to two art shows on Manhattan's West Side (not exactly "lower west side", but below midtown) that bring together mathematics and visual art in wonderful ways. One, the Frank Stella retrospective at the Whitney Museum of American Art and the other, a three-part show at The Nancy Hoffman Gallery. If you like that kind of art/math integration ("art" is how we turn STEM into STEAM!) and you have a little more energy for a longer math art walk, then I suggest you keep moving north and a bit east to hit the New York Museum of Modern Art (MoMA).
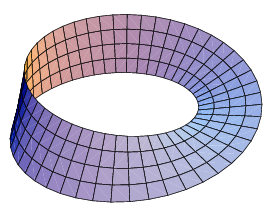
To my eye, MoMA often puts together exhibitions with mathematical connections, some obvious and some less so. At this moment, both kinds are on display. For the former, take a look at Endless House, a lovely small show of architectural models that includes homes inspired by and even named for the fundamental mathematical objects the "torus" (Preston Scott Cohen's "Torus House") and a Moebius band (the Bos/van Berke Moebius house).
Architecture has a long history of geometric inspiration and aesthetics (besides the obvious mathematical connections with engineering), going back at least to ancient Greece and the infusion of classical geometric shapes like squares and circles into their structures. Exhibitions like Endless House make apparent that the influence continues. Speaking to the title of the exhibition, both the torus and the Moebius band are examples of finite entities that still make possible the infinite. The torus is a a mathematician's wedding band, serving for many a best man's toast as the paradigm of endless love. The Moebius band is on the other hand, sort of - or almost - the wedding ring with a twist. More precisely, take a strip of paper, hold it the long way and then put in a half-twist and connect the opposite ends. Starting a one connecting edge make your way around. If you were an ant, then when you returned to the connection border you would be upside down! Keep going and when you next return, all is rightside up again - maybe that's the right metaphor for marriage....If you were an ant traveling down its center line, you would discover that eventually you were upside down. Whether orientation preserving or orientation reversing, giving the sense of infinity within the necessary boundaries of shelter is surely an architectural and mathematical aspiration.
A geometric theme continues in two other beautiful current exhibitions - but the math is a little less obvious, although in many ways much more intriguing: On MoMA's second floor you will find a concise but thoughtful exhibition sampling of the work of Jackson Pollock and around the corner, the blockbuster show of sculptures by Pablo Picasso. I'll now try to communicate what I see as I walk through the galleries wearing my math goggles.
Everybody knows Pollock for his "drip paintings", often executed by flinging paint onto a canvas placed on the floor of his studio. Pollock would literally dance about the canvas while deftly directing the paint from his brush or stick, a ballet-like dance that defined him as the original "action painter". At its best the work is a magical hybrid of intention (he had a virtuosic control of the paint, even while in motion) and serendipity. The canvas acts as a record of his movement and imagination.
To many the work of Pollock can seem, well, "random" - which is to say bereft of a recognizable pattern - but as it turns out, with a little help from mathematics, the randomness in much of Pollock's can be quantified. In 1995, the physicist Richard Taylor discovered that he could use the mathematics of fractal geometry to study Pollock's work. A "fractal image" might be described as one that exhibits surprises at every scale; that when viewed more and more closely, never completely "fills in", but that the way in which it fails at this has some regularity! That is, if you train a microscope on a fractal image, then as you crank up the power, you never get to a point where you simply see a big blob from some point on. Rather, there are always holes in the image. Furthermore, no matter how closely you look, the area covered (as viewed through the eyepiece) stays roughly the same. This area gives you a way to compute the dimension of the image, and whereas a line is one-dimensional and a filled-in region is two-dimensional, Pollock's work seems to be something in between! That is, of a fractional dimension! The mathematician Benoit Mandelbrodt invented the work "fractal" to characterize such structures and found them in all sorts of different natural (and economic) phenomena - from coastlines, to mountain ranges, from leaves to cauliflower florets. Pollock was famous for saying "I am nature" when asked about his working process. He was - mathematically speaking - right on the money.
L to R: Detail of "One 1948", J. Pollock; Detail of "white layer" of "one 1948"; Detail of Trees: Photo by Petteri Sulonen. Creative commons via PrimeJunta Flickr - See more at: http://blog.oup.com/2014/01/fractal-shapes-natural-world/#sthash.Ruaco1pB.dpuf
Interestingly, Taylor was led to this idea by his own work as an artist: as part of a final art project during a year's leave as a fine arts student, Taylor constructed a contraption that enabled him to use the wind to help him paint. He noticed that the paintings he made had some similarity to Pollock's drip paintings and that moveover, he knew that the motion of the wind (turbulence) was could generate fractal phenomena (think of the swirling patterns in the windblown smoke from a chimney). Taylor's work has not been without controversy - especially in its use for authentication (he was for a time a consultant to the Pollock-Krasner Foundation) - but the fractal computations and mathematical connections are intriguing and a delight to explore.
The big draw at MoMA right now is the exhibition of Picasso sculptures. As most know, Picasso is perhaps most often thought of as one of the founders of "cubism", an art movement of the early twentieth century that disintegrated representation of the object in favor of an explicit, if often layered or co-mingled collection of views in a single work. In this way the work makes explicit the three-dimensionality of the model the reconstruction of many many two dimensional views. In the last room of the exhibition we are told that Picasso "played with the possibility of multiple perspectives". Cubism thus becomes an artistic exploration of our stereoscopic vision which produces a 3D experience via the integration in the visual cortex of the distinct 2D views on our left and right retinae.
The most famous of Picasso's early sculptures, considered to be part of his cubist oeuvre, "Head of a Woman" (Paris, 1909) maintains this conceit of 2D layering. In the words of the work's label as written for the exhibition, the "fractured planes" and "faceted surfaces" that make up the surface of the sculpture, mark it as a cubist exploration of the medium.
In the usual historiography of cubism is presented as a natural evolutionary step from the picture planes of Cezanne. But there is another intriguing narrative, one that takes note of simultaneous developments in mathematics and physics, where the turn-of-the-century discovery of special relativity made heavy use of four-dimensional thinking to open up a whole new way of thinking about the world. In "Einstein, Picasso: Space, Time, and the Beauty That Causes Havoc" the historian of science Arthur I. Miller makes the argument that there was much discussion of the discovery of relativity in Picasso's intellectual circle, a part of a general zeitgeist around the mysteries and complexities of thinking about four dimensions. Miller makes an intriguing link (through Maurice Princet, an insurance salesman and known acquaintance of Picasso) between a popularization of four-dimensional geometry by Espirit Jouffret ("Elementary Treatise on the Geometry of Four Dimensions'', 1903), in which he gives a sense of four-dimensional objects by using multiple two- and three-dimensional "projections" - not unlike representing a three-dimensional object as a collection of planes. Jouffret's visual explanations, such as the image below, used to explain a "hypercube", are - at least to my eye - very suggestive of many early cubist works.
Jouffret was not the only one writing for the public about four dimensions. Across the English Channel, Edwin Abbott's popular 1884 math book, "Flatland" was a different attempt to bring humanize four dimensions. "Flatland" is part mathematics popularization and part social commentary and satire (complete with the cartoonish personification of geometric elements, from haughty polygons to unassuming points). Its pedagogical approach is to put the three-dimensional reader into four spatial dimensions, by analogizing our observations of the experiences of beings that would exist in two dimensions. These creatures would live as if suspended in the thinnest sheet of paper. As such, they would have no ability to conceive of a notion of "up" or "down" or "out of the paper", no more than we have the ability to imagine moving out of the world of our own spatial existence. Creatures in Flatland could be thought of as closed shapes - still embedded in the paper. However, as observers outside of Flatland - looking down on the paper - we could actually see inside the creatures! Analogously, a being that exists in four spatial dimensions could "see into" three-dimensional entities!
With this in mind, we now go back to the Picasso show. In Room 2 of the exhibition we find another of Picasso's most famous works, "Guitar" (1914) - but not a simple replication of the instrument, but rather one opened up to reveal simultaneously both its inside and outside. Suggestive of the view one might have of this guitar, if existing in four spatial dimensions.

Guitar (1914), Pablo Picasso - (http://www.pablopicasso.org/guitar.jsp)
Geometry is a subject that was born out of a human urge to understand the world around us. I like to think that art comes - at least in part - from the same urge. Here at MoMA this month, come see how the two come together in surprising and beautiful ways. While you will probably come to see the art, if you keep an open mind as you walk about, like a trip along a Mobius band, when you leave you may find yourself thinking about math.