Fans of George R. R. Martin's Song of Ice and Fire saga love to speculate about what will happen next. With two books (of seven) to go, the identity of the eventual occupant of the Iron Throne is anyone's guess.
But if the Warlocks of Qarth can see into the future, why can't we? Specifically, knowing that each chapter is told from the point of view of one character, can we use a statistical model to predict which characters will turn up next?
Cue fan outrage. Statistical models? Don't they involve randomness? Am I claiming that Martin is picking his characters out of a hat like a Dadaist poet? That he is writing chapters completely at random?
No, not at all.
A random event is one which has no cause. In real life, most things are caused by something else, but sometimes it is convenient to pretend that they are random. For example, when you flip a coin, the result is determined by the speed of the coin, the angle at which it leaves your hand, the distance it falls, and so on. But these conditions are so complicated that it is easier to say that the coin falls heads or tails at random.
Similarly, when trying to model a phenomenon, it can be fruitful to treat the more complicated parts as random and extract some sort of general trend from the rest. For A Song of Ice and Fire, I assumed that the number of point-of-view chapters for each character is completely random, but there is some structure underneath the randomness. Once the structure has been determined from the data, the model can be used to make predictions.
The predictions produced by the model are probabilities. A probability is a number which describes how likely something is to be true, given our current state of knowledge. Or in this case my current state of knowledge, probability being, according to some philosophers, something which varies from person to person.
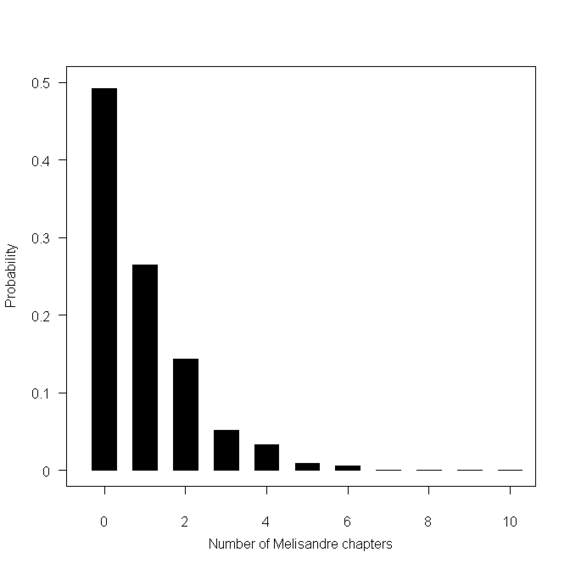
But if probability varies from person to person, how can we even say whether the model's predictions are correct? For example, if the model says that Melisandre has a 50 percent probability of having a point-of-view chapter (as suggested by the graph below) what does that mean? If the book was written over and over again, say we got 100 different versions of The Winds of Winter, then it would mean that about 50 of them would feature Melisandre. But the book only gets written once and so this notion of probability makes no sense.
A horse racing analogy helps. If Trundler has a 50 percent chance of winning the 2:30, this means that a $10 bet should pay $20 if Trundler wins. If Trundler happens to lose, that's bad luck. But if I made many such bets and lost most of them, I might begin to suspect that it was my fault. Similarly, although we will only get one book, the model makes many predictions, and we should be able to use these to evaluate the model in the same way that a gambler might evaluate a racing system.
Will it work? Probably not. Apart from not being able to use the past as an infallible guide to the future, there is the fact that the choice of model is quite arbitrary; an unquantifiable leap in the dark.
If the model is not useful, how else could we make a Game of Thrones prediction? One way would be to stick with statistics but harvest more data -- "big" data -- and, although difficult, this would probably be more effective than the "little data" approach.
In fact, the whole subject of statistics stands at a crossroads. Many of the statistical methods used in economics, health and social science are being replaced by new methods from computer science, known as machine learning or artificial intelligence. We know that the new methods are better because they can predict things which the old methods cannot.
Statisticians still talk about building models to explain phenomena, as though there were discoverable laws underlying subjects like health, education or Game of Thrones. But this is probably not the case. The complicated black-box models of machine learning explain poorly, but they often predict well. And in the real world, prediction is what matters. Physicists spent billions building the Large Hadron Collider because they care about testing the predictions of their models. A model which explains but does not predict isn't a model; it's a religion.
Who will win the battle of statistics versus machine learning? Is there room for only one subject on the Iron Throne of predictive modelling, or do both sides have something to contribute? Why does it matter anyway? It matters because predictive performance is the best way to measure whether our models are correct. If we give advice to policy makers based on incorrect models, our advice will be bad. And ultimately, if we give bad advice, people will suffer. Not just in Westeros, but in the real world too.