Some hundred mathematicians gathered at Duke University this past weekend for our annual "Festival" of the latest new results in geometry. Fernando Coda Marques of IMPA in Río de Janeiro, Brazil, reported on his new proof with André Neves of the Willmore Conjecture:
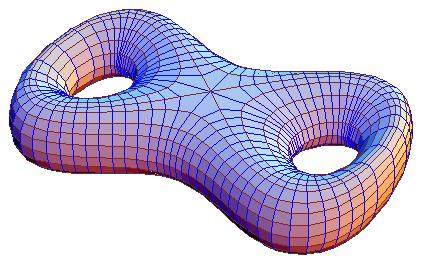
Still an open question is the optimal shape for a two-holed doughnut, perhaps something like this (click for a full-sized image):
Actually Robert Kusner of the University of Massachusetts at Amherst has a conjecture for the optimal doughnut of any given number of holes, once again based on lovely and famous twins in the parallel spherical universe, which were discovered in 1970 by Blaine Lawson of the State University of New York at Stony Brook.
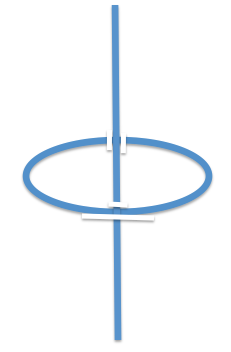
Marques also announced another, newer, related result with Ian Agol and Neves on the optimal positioning of two linked curves. You might think it best to take two linked round circles, but mathematicians have a better idea: a horizontal circle around a straight vertical line -- which mathematicians think of as an infinite circle:
Another invited speaker, Simon Brendle of Stanford University has recently proved the Lawson conjecture that Willmore's optimal doughnut's lovely twin (the "Clifford torus") in the parallel spherical universe (the "three-dimensional sphere" or hypersphere) has a special feature: it has less area than any other equilibrium doughnut. Here "equilibrium" means that the curvatures of the doughnut surface in orthogonal directions are equal and opposite. In an everyday doughnut in the familiar "Euclidean" universe, this happens on the inside, which curves inward as you go around and outward as you go up and down, but it fails on the outside, which curves inward as you go around and inward also as you go up and down. On the other hand, the lovely twin in the parallel spherical universe has such delicate equilibrium everywhere. It's more like a soap film without bubbles on a wire frame, which always curves up in one direction and down in the other. Here's how Brendle describes his proof of the Lawson conjecture for you:
The Lawson conjecture is a classical question about the shape of soap films in a three-dimensional sphere. I have long been fascinated by this conjecture, and I have tried many different approaches to the problem. However, the Lawson conjecture remained a mystery until recently, when the different pieces of the puzzle finally started fitting together.
His proof, technical but short (just seven pages long), first shows that for the least area equilibrium doughnut, the much more complicated "Gauss" curvature must be constant. Then the celebrated Gauss-Bonnet Theorem, which relates this Gauss curvature to the number of holes, implies that the Gauss curvature must be 0, which identifies it as the lovely twin of Willmore's doughnut.
In addition to Marques' and Brendle's talks and six other invited, hour-long talks, the Geometry Festival has lots of time for informal discussions over meals, snacks, and a Saturday-night banquet.
Geometry Festival organizer Hubert Bray of Duke University, this year's host institution, told me why he loves these events:
I agree.