
Spot 1: The Proposition
Let me tell you a story which does not necessarily reflect well upon me, but which led to some interesting thoughts. As we've discussed, New York magazine art critic Jerry Saltz makes himself extraordinarily available for interaction with his readers via Facebook. I've availed myself of this propensity of his in the past to sponge up a little criticism of my work.

left to right: Jerry Saltz, unidentified art enthusiast
Art critics, in one sense, play a role in the art world not unlike the role played by transistors in the electronic world. Transistors amplify signals. A transistor responds to a low-current input signal by unleashing a high-current output signal. Critics are kind of like this, as viewed from the perspective of broke-ass artists. To the broke-ass artist surrounded by paintings nobody wants to buy, attempts at getting a career going are a low-current input signal. Attention, shows, and sales are high-current output signals. The response of the critic can amplify one into the other.
From the perspective of the critic, some properties of this analogy are frustratingly true. The critic necessarily sees him -- or herself as a mechanism for directing attention toward or away from certain art objects. But for all this, the critic remains a conduit, not a primary destination. The critic doesn't make the art, and the critic usually doesn't have the money to buy the art.
Jerry Saltz, who is something of a maverick, has figured out a clever way around this problem in limited instances. Sometimes, when he has gone particularly crazy for the work of a specific artist, he has posted a call on Facebook for any of his 4,978 friends who is up for it, to make him a knock-off of the work, the trivial fee for which is only to be paid if the resemblance meets Saltz's requirements.
He did this last time he went gaga over Gerhard Richter.

I think this is the kind of Richter he meant.
I gave his call serious thought, but eventually decided that producing an original work, mimicking Richter's aesthetic sufficiently closely to match Saltz's needs, involved nailing so many formal variables that it wasn't worth the effort. So I passed.
More recently, mega-dealer Larry Gagosian, bravely resisting his native sense of understatement, opened a show of 331 of British art huckster Damien Hirst's spot paintings at all 11 Gagosian galleries worldwide:

Damien and a Hirst
Turns out, Saltz is an enthusiastic fan of the spot paintings, and once again he posted a call: Who will paint me a Damien Hirst spot painting?
Well, I thought, these paintings are so ludicrously simple-minded that it should be a snap to make one. So I told Saltz I was game, and got down to work.
Apart from the paintings seeming easy to knock off, why would I want to actually knock one off? Well, basically so I could add Jerry Saltz to my collector list. This isn't a particularly noble or even effective motive -- if anybody ever asked, I'd have to cop to the fact that the work collected wasn't me, so much as a really good copy of a Hirst. But the idea tickled me nonetheless. Richard Scott once asked, in another context, if something bizarre I had done wasn't mostly motivated by self-promotion. In that case, the answer was no. If you're reading this, Richard, this is what "mostly motivated by self-promotion" looks like.
As an aside, I am divided over whether this particular self-promotional move is awesome and hilarious, or garden-variety pathetic. You'll have to be the judge of that.
Be that as it may, I wasn't motivated by self-promotion alone. These spot paintings Mr. Hirst has done are a big deal, art-scene-wise. As far as I can tell, virtually everyone in the art world knows about them, and almost everyone loathes them, except for the people shelling out millions of dollars to own them. (And, of course, Jerry Saltz.) I thought, "These fucking things are so blank, so indifferent -- I bet if I learned them from the inside, the way you learn a piece of music from the inside by playing it -- then I would have some interesting thoughts." And I was right.

Spot 2: Thought Density
Let me clarify something which lurks around the edges of my writing, but which I don't think I've ever spelled out. My encounter with artwork triggers thoughts in my mind. I think of this process as exegesis -- the drawing out of meaning inhering in the art. Charlotte drily suggests that much of it is eisegesis -- reading meaning into bullshit. Whichever it is, much of the work I find most rewarding to consider is work that triggers many thoughts quickly: it triggers high-density thought.
One of the dimensions in which I evaluate work is the density of thoughts it inspires in me when I look at it. You may have noticed that the concept of density, of how much can be stuffed in, appears again and again in my analyses. Why? Because we're mortal. Time, thought, information - I want all of them to exhibit a maximum of density, because each of us is doomed to run out of them.
Now, looking at a Damien Hirst spot painting, I had the fairly unusual sensation of encountering something of zero thought density; a perfect thought vacuum. I shook my head, and thought, "This can't be right. Surely there is something here -- or, if I am right, how did he manage to produce something so utterly un-present?"

Spot 3: In Person
So I hied me to the two Gagosians in Chelsea, on 21st and 24th, and took a good hard look at the Hirsts they had up. A hard enough look, in fact, that a guard moseyed over and encouraged me to take a less hard look. I had gotten what I wanted -- observation that you can, in fact, see the pencil lines of the circular stencils marking out the compositions, if you stand close enough. That was important in determining the degree of precision required for Saltz's Hirst.
Standing back, I looked at the paintings:

They appeared to follow a simple set of rules:
1. Objects: circles of identical diameter
2. Arrangement: grid symmetrical about x and y axes
3. Object color: nonrepeating
The colors were going to be the hard part -- Hirst uses very weird mixed colors. I had learned from another comment of Saltz's on Facebook that he is quite sensitive to the spectrum which characterizes Hirst's work; he can recognize when a set of colors is outside the characteristic range. Therefore, I needed to nail the colors, individually and as a group, even more than I needed to nail the circle precision.
Apart from these formal concerns, and a kind of residual optical vibration when looking at those ginormo spot paintings, I really had no response at all to the work. Well, I was mildly annoyed. I think Gagosian should be showing, for instance, this:

Blue Leah #2, Daniel Maidman, oil on canvas, 24"x36", 2011
But I get that feeling every time I set foot in a Gagosian, so it doesn't really have anything to do with Damien Hirst's work.

Spot 4: Two Equations in Two Unknowns
Then I went to the studio. I had the 18"x24" canvas Saltz and I had agreed on, a ruler, and a stencil with lots of different circles on it. I was ready to go. Then I sat down to work out the sizes of gaps between the circles. I figured I had a two-equations-in-two-unknowns problem. The horizontal painting dimension, 18", had to be divided into my choice of 4 circles with three gaps, and the vertical painting dimension, 24", had to be divided into my choice of 5 circles with four gaps. All circles had diameter x, and all gaps had length y, yielding the system of equations:
4x + 3y = 18
5x + 4y = 24
Here's the revolting mess I made of working this out after not having bothered with this branch of elementary algebra in some years:

I kept getting x = 0, y = 6. It turns out there are no other solutions for this set of equations.
I tried a few other combinations (on an online two-equation/two-unknown calculator), and found that it is not so freaking easy, my friend, to find any whole-number solutions for the standard rectangles you can get at an art supply store. So I wrote to Saltz and said, "Jerry, how would you feel about a square?"
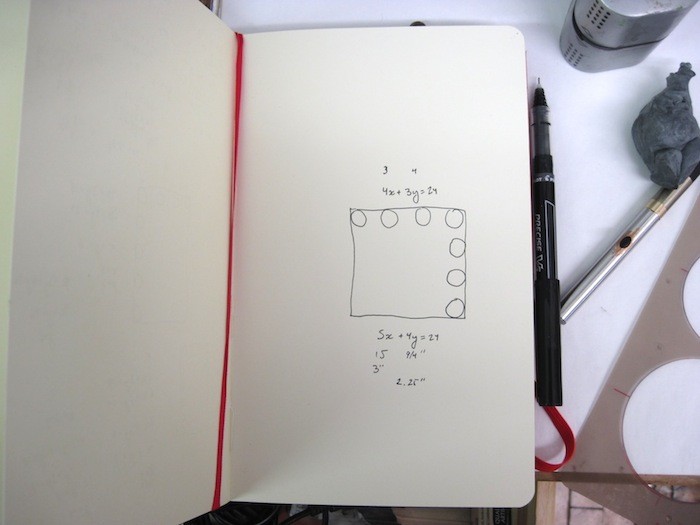
Squares are much easier to solve.
And he said, "Roberta's favorite Hirsts are the squares!" Roberta Smith, his wife, is an art critic at the New York Times.

Spot 5: How Ignoring Roberta Smith Probably Insulated Me From a Lawsuit by Damien Hirst
At the time, I hadn't gotten around to reading Smith's review of the Hirst multi-show. She mentions something which completely eluded me (and Saltz, when he examined and approved my Hirst -- no takebacks now, Jerry). I had been thinking that Hirst's rectangular spot paintings show a fairly sophisticated use of algebra, for an artist, and that he must be super-fussy about the lengths of his canvases. Not so much. Smith notes:
He is showing nothing but... smooth discs of color applied to white canvases in orderly grids at intervals equal to the diameter of the discs.1
I missed it! I just assumed that Hirst was choosing intervals not greater than the diameters of the spots. I didn't notice that they were, in fact, equal. This makes the algebra much simpler -- instead of two equations in two unknowns, its two equations in one unknown. Neither type of problem is hard, but the second is very, very simple.
So the three rules are actually:
1. Objects: circles of identical diameter
2. Arrangement: grid with intervals between circles equal to circle diameters
3. Object color: nonrepeating
In my knockoff Hirst, I assigned the intervals a length of 2.25 inches, while the circles have a diameter of 3 inches. Hirst's rule set is simple. It has three clear rules. I figure getting 1 out of 3 wrong makes me lawsuit-proof. Right?

Spot 6: Execution
I settled down and started the nerve-wracking process of getting those spots as perfect as possible. If I learned nothing else from this project, I learned a lot of respect for Hirst's assistants, who are making the actual paintings. This is tough stuff:

Getting those edges to curve properly, not jumping past the boundaries: it hurt my eyes, my back, my hand. The stress of avoiding any error, at all, gave me a headache. It really, really sucked.

I strongly recommend you don't ever set up a situation where painting and disarming a bomb swap places.
Spot 7: Nonrepetition versus Randomness
I did, however, have a fair amount of time to contemplate what this formal system was, exactly.
Consider what Hirst has set up: there are lots of variables possible in any painting. As much as is humanly possible, Hirst has eliminated variation in all but one of them. His grid is constant and symmetrical in multiple axes. His shapes are circles, which are as close to featureless regularity as shapes can get, and all of his circles are the same size. His white background is simply blank gessoed canvas, while his circles are glossy house paint, applied very evenly.
The colors, however, vary. And not only do they vary, they do not repeat -- he makes a big fuss about this. What he wants to say is that his colors are random. It is easy to mistake "nonrepetition" and "randomness" for one another. They aren't the same. Consider this pattern:
12345678
It doesn't repeat, but it's not random -- you can tell what the next digit is going to be.
Hirst himself confused the issue early in his career of producing spot paintings:
Once, an assistant painted five yellow spots in a row. ''I told him those aren't random,'' Hirst recalls. ''And we had a big fight. Now I realise he was right and I was wrong.''2
So we have a situation of zero variation in all parameters except one, which shows maximal variation, with a goal of true randomness.

Spot 8: Information Theory
What was becoming apparent to me was that, while Hirst's paintings are not interesting from the perspective of art criticism, they are very interesting from the perspective of information theory.
Information theory was more or less single-handedly founded by Claude Shannon in his 1948 paper A Mathematical Theory of Communication.3 In this fascinating piece of work, he considers how to define how much information is actually transmitted in a single unit of transmitted signal. For instance, let's say you have a transmitter that can only send a 0 or a 1. If you know that, in reality, it always sends a 1, then when it sends you a 1, it hasn't sent any information - you already knew you'd be getting a 1. Likewise, if it always sends a 0, then getting a message from it doesn't transmit new information.
On the other hand, if the transmitter is equally likely to send a 0 or a 1, then when you get a signal from the transmitter, it's something you didn't know in advance -- it's new transmitted information.
Shannon graphs the amount of information derived from receiving a single-digit signal from a 0-1 transmitter against the probability of getting a 1 out of the transmitter. The horizontal axis is p, probability, measured from 0 to 1. The vertical axis is H, amount of information, measured in bits, which, oh yeah, he motherfucking invents the bit in this paper as well:
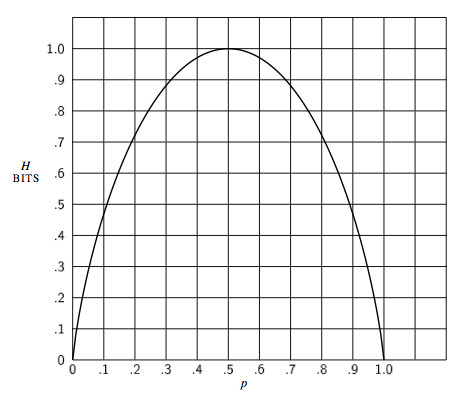
information received against probability of a 1
As you can see, the maximum amount of information received, 1 bit, occurs when a 0 and 1 are equally likely signals. This property -- how much information a system transmits per amount of signal transmitted -- he calls entropy (because he describes it using math similar to that used in physics to describe entropy). Signal entropy reaches a maximum at a 50% chance of getting a 1 out of a 0-1 transmitter.
The "opposite" of entropy is redundancy - whatever causes a system to send less than the maximum amount of information the transmission system will support. Redundancy, at its most basic level, helps to overcome transmission errors due to noise. For instance, let's say you know that 10% of transmitted information will be screwed up by your transmission wire. One way to reduce garbling of the signal is to send the same message five times in a row, so the receiver can compare the copies of the message. This produces a "consensus" value for each unit of information in the message. The procedure reduces entropy, because the receiver has a very good idea what the transmission system will be sending much of the time. But it increases redundancy, allowing compensation for noise in the system.
Now let's consider language. All languages are information systems, but not all information systems are languages. Languages transmit not only information, but meaning. It turns out that to encode meaning, redundancy is necessary. Here are a trivial and a profound example of redundancy in language:
1. The u after every q in English is redundant. Because we know that there is always a u in this position, we could easily leave it out without altering the comprehensibility of the word at all. Just ask an American how to spell "colour."
2. Examine this sentence: "I went to the store." Now take out the "went": "I [ ] to the store." If I asked you what part of speech goes inside the square brackets, you would tell me a verb goes there - you might even say a verb of locomotion in the first person singular. Because the syntax and vocabulary of the remaining part of the sentence indicates that such a verb is required by English grammar. That is, you can partially reconstruct a corrupted sequence in the message. You can do that because the presence of the verb is indicated both by its actual presence, and by the structure of the language. The system is redundant.
Language is necessarily redundant. In considering the construction of artificial languages, linguist Isabella Chiari sums up the situation as follows:
A language completely deprived of redundancy would not even have the form, needless to say the usage and communicative functions, of a language.4
Now let's get back to Damien Hirst and his three rules:
1. Objects: circles of identical diameter
2. Arrangement: grid with intervals between circles equal to circle diameters
3. Object color: nonrepeating
Let's modify the system of rules for what Hirst wants as opposed to what he accomplishes:
1. Objects: circles of identical diameter
2. Arrangement: grid with intervals between circles equal to circle diameters
3. Object color: random
This amounts to an information transmission system with 0 entropy with regard to all dimensions except color, which has maximum entropy. Remember too that language is a mix of entropy and redundancy - it needs enough entropy to allow variation, and enough redundancy to retain meaning.
The spot color system that Hirst is setting up has maximal information, which means that it must be formally meaningless. Hirst has produced a perfectly blank system. Through the lens of information theory, all responses to this system, from Saltz's delight to everyone else's revulsion, are reflections of concerns outside the system itself. The system itself is like Kubrick's monolith in 2001: it claims nothing more than that it exists.

Spot 9: Spotting the Flaw
Taking all this into account, I object to the very quality of Hirst's body of spot paintings which most engages Ms. Smith:
It seems crucial that the colors have been chosen by different people; it is part of their randomness and creates a variety that might not be possible if the paintings were made by one person. In this regard Mr. Hirst's spot paintings are more collaborations than art made by assistants. They are made not only by different hands but also by different minds, and this may be the most interesting thing about them.5
From an information-theory perspective, what Ms. Smith is describing is not randomness, but redundancy. Each assistant makes characteristic color choices and juxtapositions, causing the spot paintings, as executed, to deviate from true randomness, from maximum entropy: "This crimson spot tells me Joe the Assistant made this painting; I can assume there will be no pale pink spots in this painting, because Joe does not use that color."
I can report that these distinctions are more or less borne out by my own experience with the spot paintings (while his assistants choose the individual colors in the paintings, I suspect Hirst has carefully identified the parameters of the palette -- an oddly shaped color space, for instance, would make sincere forgeries -- unlike mine -- next to impossible to produce).
But look - is anybody going to look at a spot painting because of its aching humanity? Not unless they're autistic or schizophrenic. So when you balance one consideration -- the humanity -- against the other -- the striking information-theoretic formalism -- which facet of the spot paintings is more interesting? I think it's the formalism. And I think the flaw in the spot paintings is that Mr. Hirst, as evidenced in the episode with the five yellow spots, himself brings a residual humanity to his project which interferes with the most interesting part of its nature.
When Kubrick, also in 2001, wanted a set that was a gravity-simulating centrifuge inside an enormous space ship, did he go to set-builders? No. He went to the Vickers-Armstrong Engineering Group, which took a break from designing airplanes to help Kubrick meet his formal ambitions.
Damien Hirst's assistants' color sensibilities shouldn't be infecting his work with soul. His spots should be selected by proper random-number generators and painted by industrial robots. Hirst shouldn't be "collaborating with assistants" to make his spot paintings. He should be collaborating with Cisco and Boeing.
Oh - in case you were wondering, here's how mine turned out:

current configuration, front end of right wall of my studio
Happy birthday, Jerry! And if you're reading this, Damien, would you consider waving your 13.5" yew phoenix-tail-feather-core wand over Saltz's painting and transubstantiating it into a real Hirst? It would mean the world to him. Come on, man, it's his birthday.
SOURCES
1
Hirst, Globally Dotting His 'I'
Roberta Smith, New York Times, Jan. 12, 2012
http://www.nytimes.com/2012/01/13/arts/design/damien-hirsts-spot-paintings-at-gagosian-in-eight-cities.html?pagewanted=all
2
Completely dotty
Carol Vogel, Sydney Morning Herald, Jan. 21, 2012
http://www.smh.com.au/entertainment/art-and-design/completely-dotty-20120119-1q712.html#ixzz1mHASFSSU
4
Redundancy Elimination: The Case of Artificial Languages
Isabella Chiari, Journal of Universal Language 8, September 2007, 7-38
www.unish.org/unish/DOWN/PDF/8_2_1.pdf
In case you're wondering whether a set of colored circles can ever form a language, consider the vocabulary of train line identifiers for the New York City subway system, and their grammatical use in giving trip directions.
5
Smith, op. cit.
6
Not quoted in the post, but the starting point of this adventure - Jerry Saltz on Damien Hirst:
http://www.artnet.com/magazineus/features/saltz/damien-hirst-gagosian-1-13-12.asp