
After a 47-year search, mathematicians Fernando C. Marques and André Neves have found the best doughnut, or at least the best geometric shape for a doughnut, pictured in Figure 1, with the narrow hole only about 17 percent (3-2√2) of the width of the doughnut. "Best" for mathematicians means the least bent out of shape, minimizing a physically natural elastic bending energy like certain cell membranes (defined mathematically as the integral of the mean curvature squared).
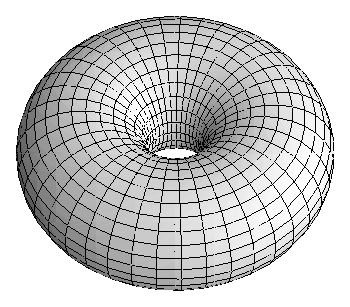

Figure 1. Mathematicians prove that the best doughnut has a small hole (top image courtesy of geom.uiuc.edu/~banchoff, thanks to Tom Banchoff, all rights reserved; bottom image courtesy of Wikipedia creative commons).
The 47-year-old puzzle is called the Willmore Conjecture. It is named after the English geometer Thomas J. Willmore.

Thomas J. Willmore (photo by John M. Sullivan, used with permission, all rights reserved).
Willmore guessed the best shape in a 1965 paper. He died February 20, 2005, seven years, almost to the day, before its solution. The solvers hail from a premier mathematics institute (IMPA) in Río de Janiero and Imperial College, London. They posted a preprint of their 96-page proof on the arXiv on Feb. 27, 2012.
A key to the proof is moving the problem from ordinary, three-dimensional space to a three-dimensional spherical universe that closes back on itself, a three-dimensional analog of the Earth's surface, where you don't have to worry about things disappearing off to infinity. There they consider the closely related problem of minimizing area, a contest in which our best doughnut is distinguished only as a sixth-class competitor (with a five-dimensional space of instabilities). The theory of such hybrid "mini-maxima" was developed by my own late thesis advisor Fred Almgren, of Princeton University, and his Ph.D. student Jon Pitts, now of Texas A&M.
Actually there is not just one optimal shape; there are infinitely many equally good shapes, all related by certain "conformal" symmetries, as in Figure 2. Such "Dupin cyclides" are being used in modeling and architecture, where they piece together to design beautiful structures. Maybe Dunkin' Donuts will be interested.

Figure 2. Mathematicians are equally happy if the hole is moved "conformally" off to one side (image courtesy of chem.ucla.edu, thanks to Xavier Michalet, all rights reserved).