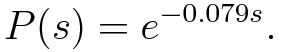There are still 12 days left in February, and since we've already logged the snowiest month since record-keeping began in 1872 (45.5 inches of snow... so far), every Bostonian is thinking the same thing: how much more snow will we get?
We can answer that question with math, but we need to rephrase it just a bit. Here's the version we'll work with: what's the probability that Boston will get at least s more inches of snow this month? The answer is the function
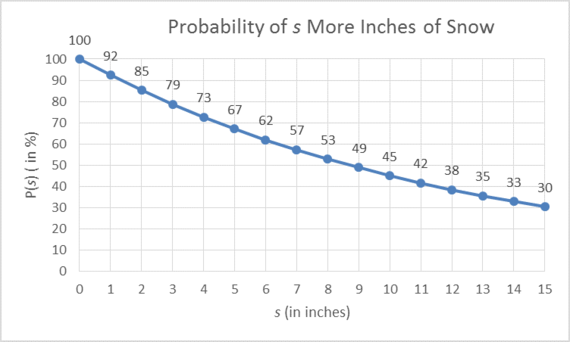
For example, to find the probability that we'll get at least 5 more inches of snow substitute s=5 and calculate e^(-0.079(5)). The answer is about 0.67, or 67 percent. (Ugh, that's pretty high!) The graph of P(s) is just as much of a downer:
(Note: the outputs -- 100, 92, 85, etc. -- have been rounded.) Unfortunately, the math predicts a 50/50 chance Boston will get about another 8.6 inches (!), and about a 30 percent chance we could see at least 15 more inches!!
The only good news I have is that the P(s) function is not exact. Though I did use historical snowfall totals for February (the data I used goes back to 1920), I also fitted a curve to that data, which generates some error. (More advanced methods could reduce the error.)
Putting aside for the moment the possible error in the calculation and the disappointing results, I hope you agree that this type of analysis is really useful. I also hope it encourages you to brush up on (or learn) calculus, because that's what made the analysis possible (along with some probability theory too). I've put the details of the derivation here, where it's easier to display equations. But if you don't make it there, I'd like to leave you with one last useful equation: math + Microsoft Excel + the internet = powerful stuff.