Can you think of a shape that occupies three times as much area on a page as it used to, when it's doubled in size? We'll provide a flaky answer later on.
Did you know that to check the accuracy of claims such as "he's twice the man his brother is" all you have to do is verify that the big fellow is 26% taller (and wider and deeper) than his diminutive sibling?
Perplexed? Let's start with something easier to get your teeth into: fruit.
Consider the orange image. The item on the left is almost one and a half times as wide as the one on the right, yet it's twice as big as the smaller one.
Now consider the apple image. The item on left is only one and a quarter times as wide as the one on the right, yet it too is twice as big as the smaller one.
What's going on here? It all depends on how you slice it: while these could be orange halves and apple halves---the former facing us, the later facing away---it's actually orange slices and whole apples that are depicted above.
Maybe those old warnings about apples and oranges comparisons have some merit after all.
What about the two ripe red tesseract buds below, which introduce a whole new dimension of flavor? You guessed it, you can double your pleasure and double your fun with the one on the left, though this time the larger one only appears to be a bit bigger than the smaller one.
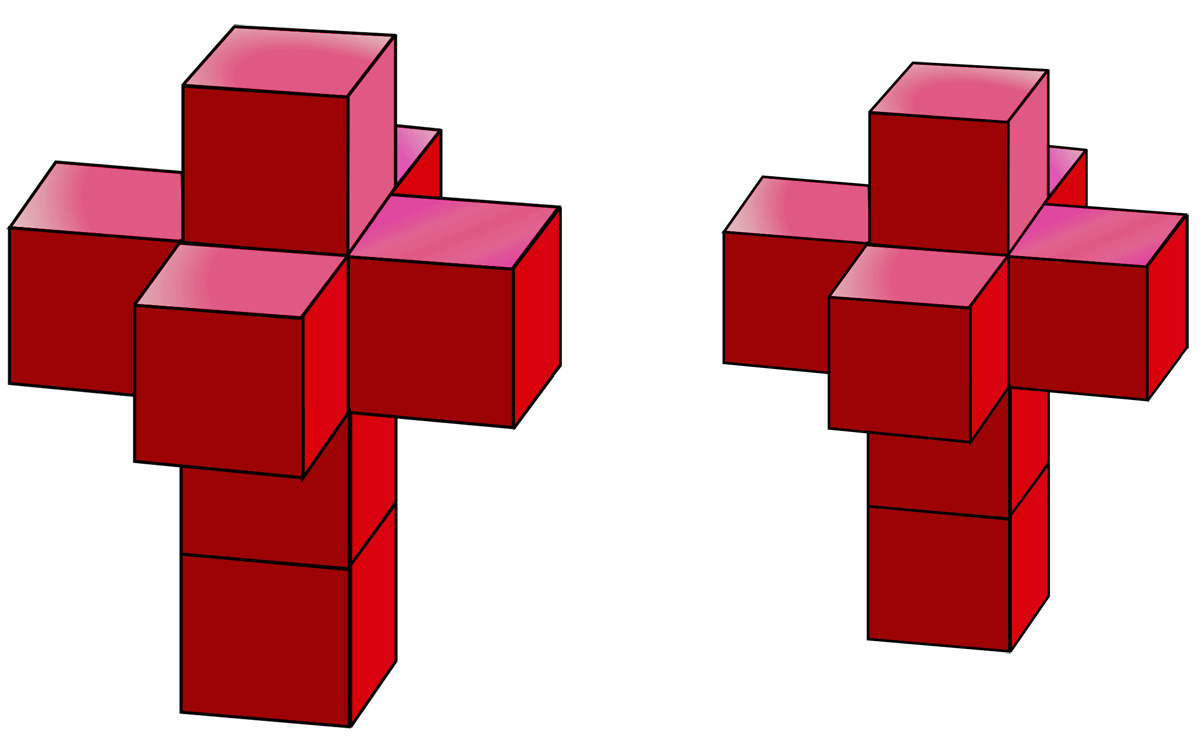
In each case it's the actual piece of fruit that is twice as large. For the orange slices (assumed to be of the same thickness), it's basically area that is doubled, and for the apples, it's volume.
The slightly sneaky part is that this fruity duplication is achieved via more modest increases in width: by a factor of about 1.41 in the case of the orange slices, and by a factor of about 1.26 in the case of the apples. We'll explain where those factors come from shortly.
The mathematics behind these claims is easier to see if we first focus on the easiest building blocks of area and volume, namely, squares and cubes.
The larger square above is four times as large as any of the smaller squares from which it is made up, although it's only twice as wide as any of those.
Similarly, the cube below is eight times as large as any of the smaller cubes of which it is composed, though again only twice as wide as one of those.
The real reason that those size differentials are 4 and 8, respectively, is that squares are 2-dimensional (and 4 is 2 squared, namely 2 times 2), whereas cubes are 3-dimensional (and 8 is 2 cubed, namely 2 times 2 times 2).
If we want one square (or cube) to be exactly twice as big as another one, we have to construct it more carefully.
The blue square on the left above is twice as large as the one to its right, and the cubical cardboard box on the left below is twice as large as the one to its right.
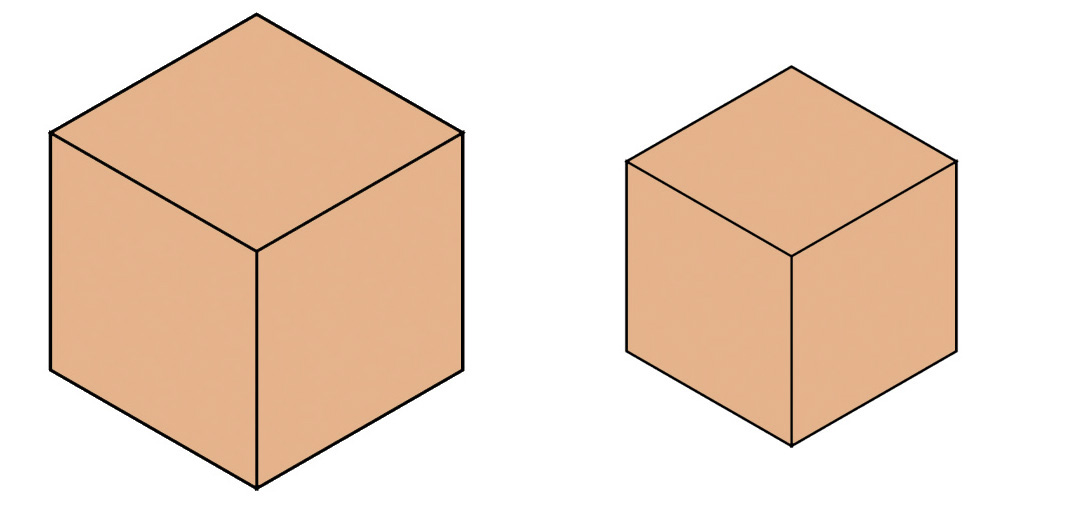
However, we can no longer justify these claims with dissections into smaller squares or cubes---no matter how many we use---but area and volume formulas help.
If the smaller blue square has unit width, and the larger one has width W, then the larger one has area . For this to be twice the area of the smaller one, W must be the square root of 2, which is 1.4142 (approximately). This all scales up or down, so that no matter what the width of the smaller square, the larger one is about 41% wider than it. Note that the square root of 2 is also the length of the diagonal of a unit square.
Similarly, if the smaller cubical box has unit width, and the larger one has width W, then the larger one has volume . For this to be twice the volume of the smaller one, we must have W equal to the cube root of 2, which is 1.2599 (approximately). This too scales up or down, and no matter what the width of the smaller cube, the larger one is about 26% wider than it. If you've packed and moved a few times, this may not come as such a big surprise.
The same considerations apply to circles and spheres, hence our initial orange slice and apple comparisons: the larger orange slice is 41% wider than the smaller one, whereas the larger apple is only 26% wider than the smaller one. This is because area and volume for these shapes is proportional to the square and cube, respectively, of width. Nevertheless, the two larger items are actually twice as large as their smaller counterparts.
We can also imagine extra large slices 
and whole fruits 
(click to enlarge) which are each twice as wide as their smaller neighbours, and hence four and eight times as large, respectively, when area or volume is taken into account. However, unlike in the earlier rectangular cases, here we cannot view the larger items as being composed of four (or eight) smaller objects of the same shape.
One might ask if there is any fruit for which "twice as big" is more intuitive, and doesn't require square or cube roots? Straight bananas of the same girth would be easy to compare: a 6 inch long sample really would be twice as big (and twice as heavy) as a 3 inch one. Of course if the girth is also expanded or contacted in proportion to the length, we'd be back to the 3-dimensional situation as for whole oranges and apples, or strawberries or berries in general. Incidentally, straight (but not narrow) bananas were the subject of a slippery European Union directive (No. 2257/94) in 1994.
Now we return to those tasty tesseract buds shown earlier.
These are in fact 3-dimensional projections (of a particular type) of hypothetical fruit living in hyperspace. A Tesseract is a kind of shadow of a 4-dimensional square or cube, namely the next step in the sequence "line segment", "square", "cube", .. . There are other ways to visualize hypercubes in 3-dimensional space. For the tesseract images shown above, where true size is measured by 4-dimensional volume, the image on the left is only 19% "wider" than the image on the right, yet twice as big as it.
True 4-dimensional hypercubes can be assembled from "space plans" like the tesseract image on the right below, appropriately folded up in the fourth dimension, just as cubes can be assembled from "floor plans" like the image on the left below, when folded up correctly in the third dimension. (That's what Salvador Dali had in mind in his 1954 Corpus Hypercubus painting.)
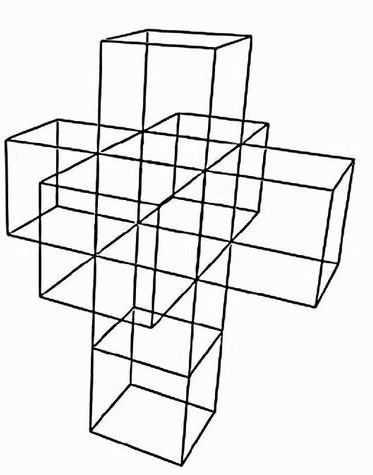
Assuming the smaller red tesseract from before has unit "width" (the size of any of its square components), and the larger one has width W, then the larger one has (hyper-)volume . For this to be twice the volume of the smaller one, we must have W equal to the fourth root of 2, or 1.1892 (approximately). This too scales up or down, and no matter what the "width" of the smaller tesseract, the larger one is about 19% "wider" than it. Can you guess the length of the "diagonal" of a unit tesseract, even if you can't visualize it? Hint: first find the length of the diagonal of a unit cube, using Pythagoras Theorem twice.
Here's the general rule for doubling size:
If a D-dimensional object of unit "width" is to be doubled in size,
then its "width" should be increased to .
This is the root of the problem: we have to extract the D-th root of 2 to solve the equation for W.
"D-volume" is length if D = 1, area if D = 2, and volume if D = 3. In those three cases, the width should be increased 100%, 41% and 26% respectively. For D = 4, in order to double hypervolume, the width increase factor drops to 19% .
That formula can also be put to use for our final, less intuitive, example.
As Keith Devlin has pointed out, over and over, we need to take a broader view of multiplication and exponentiation than as repeated addition and multiplication, respectively. The formula just highlighted applies in cases far removed from that simple world, or the convenient building blocks encountered above.
The new image on the left below is twice as big as the one on the right, while being about 73% wider.
Curiously, as we'll shortly see, the 2-dimensional space occupied by it (and its interior) is exactly three time as large as the corresponding area taken up by the smaller image.
These images depict the same "infinite level of detail" fractal known as the Koch snowflake, scaled appropriately. Its dimension is not a whole number! It's somewhere between 1 and 2, and is a measure of the snowflake's "between curve and surface" status. (Edible incarnations of this pattern can only be dreamed of, perhaps involving infinitely delicate and detailed pastry work, and incredibly finely powdered sugar.)
An approximation for the expansion factor 1.732051 required for doubling the size may be obtained by plugging the exact dimension D = log(4)/log(3) into the formula. Alternatively, given that expansion factor, then an approximation for this dimension, namely, 1.2619, can be deduced (using logarithms) from the above formula.
Why roughly 1.732? Squaring that suggests something which can be verified using information just provided, and a little algebra: the larger snowflake does indeed occupy exactly three times as much area on a page as the smaller one, counting the interiors, yet it's strictly speaking only twice as big as it!
Please note that even mathematically inspired Apples in stereo---real 3-dimensional musicians---must be increased by a non-Pythagorean scaling factor of 26% to double in size from what's shown 
here to what's shown 
here.
How about them Apples?
For additional head-scratching thoughts on squares and circles in various dimensions, click here.
Further food for thought is also only a click away. Since that was written, Vi Hart's finger licking hexaflexamexigon video , the fourth in a series on a kind of "flat, two-dimensional" object whose precise area is not so obvious, has gone viral. Can tesseract tacos or fractal fajitas be far behind?
Thanks to TinRoof Marketing & Design and Spelman College's Dan Bascelli for graphics production and assistance. Thanks to Thorsten Fleisch for cube and tesseract skeleton images. All images used with permission.