Artistic inspiration comes from anywhere even painting by numbers. However, in this case, the numbers are a table or matrix of numbers. How? First, take a look at this image that was part of the mathematical art exhibit at the Bridges conference which celebrates connections between math and art.
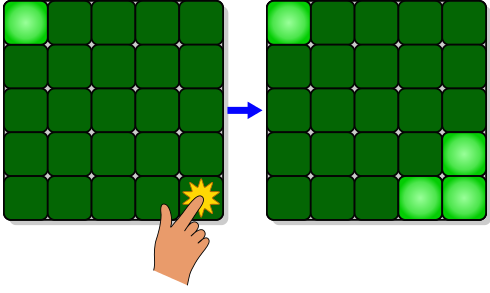
To understand this portrait, created by Dr. Bruce Torrence of Randolph-Macon College, you need to know the Lights Out game. We'll play on a 5 by 5 grid of lights. When the game starts, a random number of these lights is switched on. In the game below, the upper left light is on.
Pressing any of the lights will toggle it and the adjacent lights. For example, pressing the lower right light, as seen below, toggles the lights above and to the right.
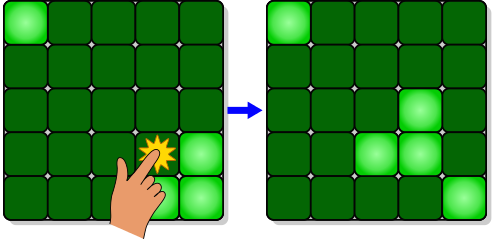
If we then press the light in the fourth row and fourth column, the puzzle becomes the configuration seen below. Why all the toggling? The goal of the puzzle is to switch all the lights off, preferably in as few button presses as possible.
This puzzle lies behind Torrence's portrait of Tibor Gallai seen above. Gallai, a Hungarian mathematician, was the first to prove that for any sized grid in the Lights Out game, it is always possible to get from the all-on to the all-off state.
Where are the numbers in this art piece? The portrait is pieced together from 28 by 28 squares which come from reachable states of the Lights Out game on a 28 by 28 grid of lights. How do you know which configurations of lights can be acheived in a game? That's where Torrence used math and equations. A 28 by 28 grid becomes a 28 by 28 grid of numbers where 1 and 0 correspond to a light being turned on and off. From linear algebra, we can multiply matrices together and such multiplication gives Torrence all possible states which becomes his pallette.
Want to create some mathematical art? Here's a quick way from my Massive Open Online Course offered through DavidsonX, a partnership between Davidson College and edX. Like Torrence's work, it uses linear equations. Probably the most well-known linear equation is y = mx + b, leading to the graph of a line. We can do the same thing but at the pixel level. Let's take a grayscale image, like that of the Mona Lisa shown below to the left. Now, let x be the value of the pixel. Choose m and b and you get a new pixel value when you apply y = mx + b. For example, take m = -1 and b = 255. If your pixel is 25, then the new value is -25 + 255 = 230. Applying this to every pixel, we get the new image shown below to the right.
We can also work with color images. In this case, every pixel contains 3 values - red, green and blue intensities which combine to color the pixel. Choose m and b for the red, green and blue color channels and you get a new pixel value. For example, let's recolor with r - 80, where r is the intensity of the red channel. Let the new green channel equal -0.75g + 150 and finally the blue intensity equal -0.5b + 200. Here's the result when we start with a color image of the Mona Lisa.
Got ideas? Visit the Image Linear Color Transformation page to upload your own image and try your own equations just like the students in my DavidsonX course.
Want to know more? You can visit the DavidsonX page and read more about the course which is running in archived mode now. Or, you can look at my book When Life is Linear: from computer graphics to bracketology and learn this and other ideas in image manipulation.
For now, what comes to mind! Create your own equation and become your own mathematical artist!