Co-authored by by David Borland and Tabitha Peck
In just over 90 minutes, audiences from young to old feel numerous emotions watching Pixar's Inside Out. While such an emotional reaction fits the film, this experience isn't new, at least for many of us. Think of a Pixar character, possibly Nemo, Woody, or now Joy, and you can probably also think of emotions you felt during that character's tale. What goes into making such characters? An important step is creating storyboards, like the one below drawn by Inside Out Story Supervisor Josh Cooley, which pre-visualize the film. The sketches are placed side by side in sequence, so that they convey scenes and deliver a rough sense of how the story unfolds. This storyboard is one of approximately 177,096 drawn for the film.
Of course, Pixar films are computer animated so such drawings must be represented in 3D in a computer. This is done with wireframes, like the one below for the set of Headquarters, the control center inside Riley's mind.
If you were to zoom in, you'd see there are sharp corners in the wireframe at the edges. However, if you were to look at the final rendered image below, you'd find the edges have been smoothed. This is especially important in character design like those placed in the set below. How does Pixar create smooth surfaces from its initial wireframes? Simply put: mathematics! In fact, an important step uses weighted averages. Did you ever compute your final (or potential) grade for a class where quizzes might be worth less than tests? Weighted averages played a role. Let's see how Pixar uses such math as part of its animated storytelling movie magic!
Pixar's short film Geri's Game (1997) demonstrated their weighted-average based subdivision technique, which continues to be used in Pixar films today. Subdivision smooths a wireframe mesh, visible in Geri's hand below to the left, by subdividing each polygonal face of the mesh into smaller and smaller faces to give the appearance of a smooth surface, visible below to the right.
To understand subdivision, let's see how it works in 2D. We'll begin with a square as seen below to the left. Then, for each line segment, find the midpoint, which is in fact the average of the two endpoints of the line segment. This step is called split and is seen with the new black circles below to the right.
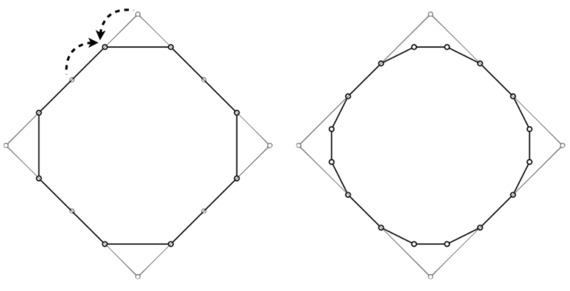
Next, we replace the original vertices of our square with points found by a weighted average. To begin, we'll use a 1-1 weighted average, also known as the 1-1 rule. That is, our original vertices and midpoints are each given the same weight. In the clockwise direction, we replace each vertex of our square with the average of its value and the next midpoint. This creates a subdivision of our original polygon, now with eight points as seen below to the left.
We can repeat this process. We split the new line segments to find the midpoints, then in the clockwise direction we replace each vertex of our current polygon with an average of the vertex and the next midpoint. If we continue to loop through this process, we get a smoother polygon via subdivision, as seen in the image below to the right. This is precisely how Pixar goes from a coarse wireframe to a smooth model, only they do it in 3D instead of 2D, as with Geri's hand.
Want to try it yourself? Visit the subdivision web app and you can. You can try other weights with the web app so let's try a 1-2-1 weighted average, or the 1-2-1 rule. That is, for each vertex, we take the average of the two adjacent midpoints, one in each of the clockwise and counter-clockwise directions, along with 2 parts of the vertex's location itself. Repeated applications of the 1-2-1 rule gives the image below to the left.
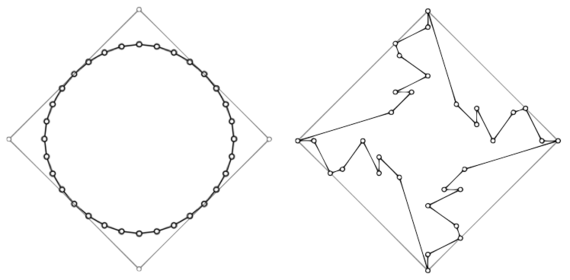
This looks pretty similar to what we produced with the 1-1 rule, as both result in smooth images. Be careful though. Not all coefficients are the same. Consider using the 1-(-2)-3 rule, where we take 1 part of the counter-clockwise neighbor, -2 parts of the vertex itself, and 3 parts of the clockwise neighbor, as indicated in the rule. On a square, you get the image above to the right after a few applications. This rule results in a "curve" which is nowhere smooth.
So, how do you know what to use? If you want something guaranteed to be smooth, take a row of Pascal's Triangle? Remember that? The first row is 1. The second row is 1-1. The third row is 1-2-1. The next row is 1-3-3-1, which you could try for coefficients. What else might you try? That's for you, in your own mathematical studio, to try. Visit the subdivision web app, and try your own coefficients. Try beginning with something other than a square, possibly with more points. What happens?
Have fun and see what you get! And remember, it's mathematics helping produce those wondrous animated images that leave such long-lasting memories that we hold for years to come.