
When Prince Fielder hits that final long ball in the World Series and knows he needs the home run, what is his fastest path around the bases? If he runs straight for first, he either has to slow to a near stop or go sailing far beyond into the outfield. The standard recommended ''banana'' path follows the baseline maybe halfway and then veers a bit to the right to come at first base from a better angle to continue toward second. That cannot be ideal. It would have been better to start at an angle to the right to head directly to an outer point on the banana path. So what is the optimal path? Using a very simple model, my colleagues and I obtained this path:
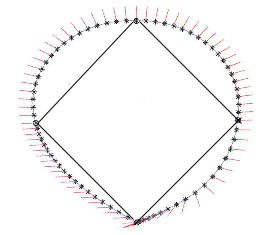
You start out heading about 25 degrees right of the base line and run with acceleration of constant maximum magnitude. You slow down a bit coming into first, hit a local maximum speed as you cross second, start the final acceleration home a bit before crossing third base, and reach maximum velocity as you sprint across home plate. The total time around the bases is about 16.7 seconds assuming maximum acceleration 10 feet per second per second, about 25 percent faster than following the baseline for 22.2 seconds (coming to a full stop at first, second, and third base), and about 6 percent faster than following a circular path for 17.8 seconds. The record time according to Guiness is 13.3 seconds, set by Evar Swanson in Columbus, Ohio, in 1932. His average speed around the bases was about 27 feet per second.
Is it legal to run so far outside the base path? The relevant official rule of Baseball says:
7.08 Any runner is out when -- (a) (1) He runs more than three feet away from his baseline to avoid being tagged unless his action is to avoid interference with a fielder fielding a batted ball. A runner's baseline is established when the tag attempt occurs and is a straight line from the runner to the base he is attempting to reach safely.
The rule just says that after a tag attempt the runner cannot deviate more than three feet from a straight line from that point. The rule doesn't apply until the slugger is almost home, when our fastest path is nearly straight. So our path is legal.
The model's only assumption is an upper bound on the runner's acceleration vector, which we take to be 10 feet per second per second for the times given here. For a better runner the acceleration might be greater and the times correspondingly faster, but the optimal path is the same. The markings around our optimal paths show the acceleration, forward at the beginning and end, leftward for most of the path.
The fastest path to second base is more symmetric, because you start from rest at home and you must come to rest on second base. So the path veers outward just as much from home to first as from first to second, starting at a larger 28 degrees to the right of the baseline. It takes 10.4 seconds (assuming acceleration of 10 feet per second per second), as compared to 12 seconds along the baseline, coming to a full stop to make the sharp turn at first and second base.
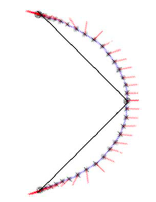
The fastest path to third base is also symmetric, with the big bulge between first and second and a smaller initial angle of 23 degrees right of the baseline. It takes 14.5 seconds, as compared to 18 seconds along the baseline, coming to a full stop at first, second, and third base.

This work began with a colloquium talk I advised at Williams College by undergraduate Davide Carozza:
My colleague Stewart Johnson was in the audience. He realized that he could compute the fastest path accurately, as pictured above.
This post is based on our article in The Mathematical Intelligencer. For more information, see my personal blog.