"But this technology has been around for years now!" That's the refrain I commonly hear these days when talking to more seasoned AI practitioners about the resurgence of AI and machine learning.
The origins of many of the scaled machine learning techniques in vogue today can be traced all the way back to the advent of computing in the late forties.
Breakthroughs in scaling Artificial Neural Networks (ANNs) have led to a resurgence of interest and much wider application of these techniques, now better known as Deep Learning.
So, what other technologies are primed for a resurgence?
How about Evolutionary Algorithms?
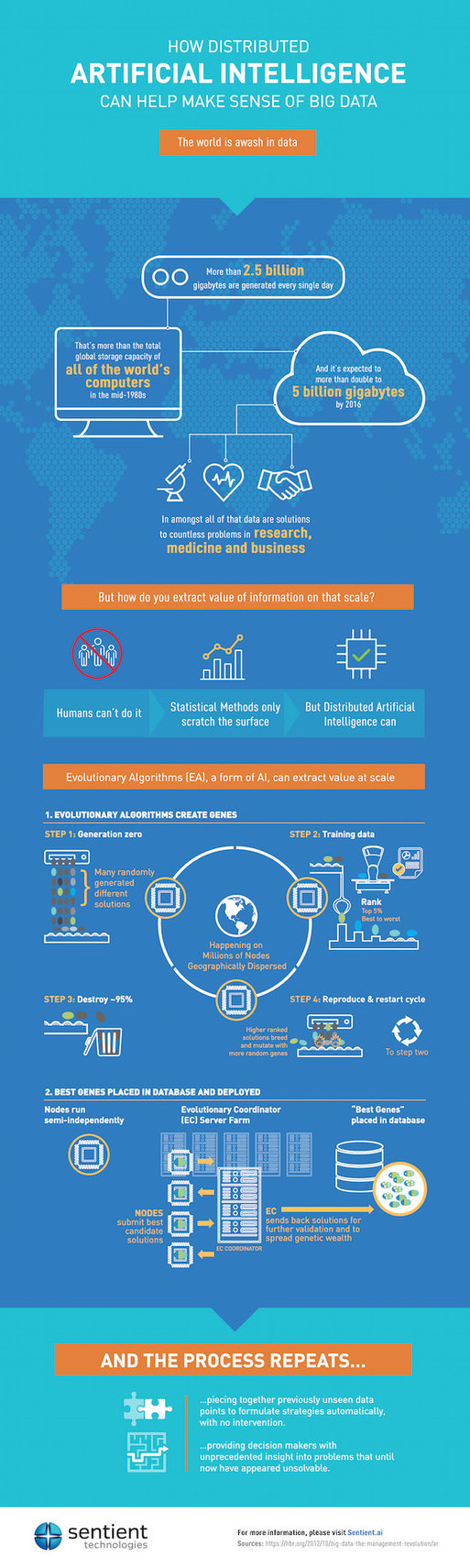
Like ANNs, Evolutionary Algorithms (EAs) are techniques inspired by models of biological intelligence, applied to real-world problem solving. In the case of EAs, the approach is population-based.
Here's how it works: A model of the desired outcome is used for producing candidate solutions otherwise known as genes. For example, let's say we are given ten numbers and the task is to order them from smallest to largest.
The model for the desired outcome is a list of size ten that includes all ten numbers. In other words, as long as we have a full list of ten numbers, in any particular order they may be, we have a candidate.
The system then generates a population of such candidates, all of which comply with the model, but that differ with one another. To generate this population, the easiest thing to do is to throw dice, and generate the candidates randomly (step 1).
It is likely that none of the candidates generated in the first go round are our solution, because none are ordered from smallest to largest. However, some are closer to the solution than the others. In other words, some seem to be more ordered.
One way to measure how "ordered" the lists are with respect to one another is to go through each list and count how many times we run into a number that is not greater than the prior number. This method of measuring the relative distance of the candidates from the solution is called a fitness function, and it helps the system rank order the candidates in the population based on "fittest" to "least fit" to be the solution (step 2).
The most famous type of EAs are Genetic Algorithms (GAs), first introduced by John Holland in the late seventies. He introduced the notion of directing the random generation of candidates so as to give the fitter candidates from a preceding population a larger role in the generation of new candidates. In our example above, for instance, rather than generating a new candidate completely randomly all the time, we would occasionally take one of the fitter lists and make a minor change to it -- like swapping two of the numbers at random. This is known as the mutation operator, and it could go both ways. If we are lucky, and the system randomly picks two numbers to swap that were in the wrong order then the resulting "offspring" candidate will have a better fitness.
Like in nature, however, most mutations are not beneficial. But mutations are quite useful, because in the rare occasions when they do improve a candidate's fitness, they can result in new global optimums. They can also help diversify the population of the fittest candidates while maintaining most of the traits.
Another reproductive operation popularized by Holland is the crossover. For this one, two "parent" candidates are selected, from the fitter candidates in the population, and they are merged into at least two offspring -- the idea being that at least one of the two would turn out to be fitter than the parents (step three). In our example, we would pick, say, the first and third lists as parents, we would then pick a few numbers from one of the parents and copy them into the offspring, and to complete the offspring's list we would take the remaining numbers in the order they appear in the second parent.
The first thing that struck me, and I suspect many other practitioners, as fascinating about evolutionary algorithms, is the fact that they often work, and sometimes produce unexpected results -- a delight that seems to be the hallmark of AI systems. Like ANNs, these simplified simulations seem to prove out our models of how nature operates, and, I think, this was the main impetus and drive behind the initial adoption of these methods.
Like ANNs, the use of EAs hit a slump once people realized that they do not scale as easily to solve large real-world problems, and simpler methods such as Support Vector Machines, prevailed.
Scaling a Machine Learning algorithm requires the ability to run the algorithm on many machines/processors, but that is not the only requirement: the algorithm should be able to actually make productive use of the distributed processing capacity. An evolutionary algorithm is "embarrassingly parallelizable." After all, an evolutionary system is comprised of a population of individual candidates which can each be validated independently.
John Koza, a student of Holland's, was one of the first to exploit the parallelizability of EAs in order to scale his system. He used a cluster of 1000 CPUs to run EAs for automatic circuit design. His system was able to reinvent 15 logic circuits patented between 1917 and 2001, and 9 which may well be patentable (including algorithms for quantum computing).
In his 2003 book, Milestones in Computer Science and Information Technology, Edwin D. Reilly noted that "Genetic programming holds the greatest promise for eventual development of a computer that can pass the Turing test. And this would be the very way that Turing himself envisioned that it might happen." In fact, Koza inspired an annual competition, called the Humies, for Human-Competitive Results Produced by EAs.
So are EAs primed for resurgence now? It is quite possible that, by virtue of their distributability, EAs emerge as the next big thing in AI, allowing us to tackle more ambitious problems.